正交/双重机器学习
它是什么?
双重机器学习是一种用于估计(异质)处理效应的方法,适用于所有潜在的混淆变量/控制变量(同时对收集数据中的处理决策和观测结果有直接影响的因素)都已被观测到,但这些变量要么数量过多(高维),导致经典统计方法无法应用;要么它们对处理和结果的影响无法通过参数函数(非参数)令人满意地建模。后者的这两个问题都可以通过机器学习技术来解决(参见例如 [Chernozhukov2016])。
该方法将问题简化为首先估计两个预测任务:
根据控制变量预测结果,
根据控制变量预测处理;
然后,该方法在最终阶段估计中结合这两个预测模型,以建立异质处理效应模型。这种方法允许为这两个预测任务使用任意机器学习算法,同时最终模型仍能保持许多有利的统计性质(例如,较小的均方误差、渐近正态性、置信区间构建)。
我们的软件包为最终模型估计提供了几种变体。其中许多变体还提供了有效的推断(置信区间构建),用于衡量学习模型的不确定性。
有哪些相关的估计器类?
本节介绍在这些类中实现的方法:_RLearner、DML、LinearDML、SparseLinearDML、KernelDML、NonParamDML、CausalForestDML。点击这些链接可以查看每个类的详细模块文档和输入参数。
何时使用?
假设您拥有观测(或来自 A/B 测试的实验)历史数据,其中选择了一些处理/干预/行动 \(T\) 并观测到了一些结果 \(Y\),并且所有可能影响 \(T\) 的选择并同时对结果 \(Y\) 有直接影响的变量 \(W\)(也称为控制变量或混淆变量)也记录在数据集中。
如果您的目标是了解处理对结果的影响,以及这种影响如何作为处理样本一组可观测特征 \(X\) 的函数而变化,那么可以使用此方法。例如,调用
from econml.dml import LinearDML
est = LinearDML()
est.fit(y, T, X=X, W=W)
est.const_marginal_effect(X)
通过这种方式,可以通过简单地检查哪些 \(X\) 的效应为正来学习最优处理策略。
提供的大多数方法都对异质处理效应模型进行了参数形式假设(例如,在一些预定义的;可能是高维的;特征化上是线性的)。这些方法包括:DML、LinearDML、SparseLinearDML、KernelDML。对于完全非参数的异质处理效应模型,请查看 NonParamDML 和 CausalForestDML。有关非参数 CATE 估计器的更多选项,请查看 基于森林的估计器用户指南 和 Meta Learners 用户指南。
形式化方法概述
该模型对数据生成过程做出了以下结构方程假设。
DML 尤其吸引人的地方在于,它对 \(g\) 和 \(f\) 没有进一步的结构假设,并使用任意非参数机器学习方法对其进行非参数估计。我们的目标是估计常数边际 CATE \(\theta(X)\)。
估计 \(\theta(X)\) 的思路如下:我们可以将结构方程重写为
因此,如果可以估计条件期望函数(这两个都是非参数回归任务)
然后我们可以计算残差
它们随后由以下方程关联
随后,由于 \(\E[\epsilon \cdot \eta | X]=0\),估计 \(\theta(X)\) 是一个最终的回归问题,将 \(\tilde{Y}\) 对 \(X, \tilde{T}\) 进行回归(尽管模型在 \(\tilde{T}\) 中是线性的),即
文献中的多篇论文已对这种方法进行了分析,针对不同的模型类 \(\Theta\)。[Chernozhukov2016] 考虑了 \(\theta(X)\) 为常数(平均处理效应)或低维线性函数的情况,[Nie2017] 考虑了 \(\theta(X)\) 属于再生核希尔伯特空间 (RKHS) 的情况,[Chernozhukov2017]、[Chernozhukov2018] 考虑了高维稀疏线性空间的情况,其中对于一些已知的高维特征映射,\(\theta(X)=\langle \theta, \phi(X)\rangle\),且 \(\theta_0\) 只有很少的非零项(稀疏),[Athey2019](及其他结果)考虑了 \(\theta(X)\) 为非参数 Lipschitz 函数并使用随机森林模型拟合该函数的情况,[Foster2019] 允许使用任意模型 \(\theta(X)\) 并基于模型空间的样本复杂度度量(例如,Rademacher 复杂度、度量熵)给出结果。
DML 的主要优势在于,如果对 \(\theta(X)\) 做出参数假设,那么可以实现快速估计率,并且对于许多最终阶段估计器的情况,第二阶段估计 \(\hat{\theta}\) 也能实现渐近正态性,即使第一阶段对 \(q(X, W)\) 和 \(f(X, W)\) 的估计在 RMSE 方面仅是 \(n^{1/4}\) 一致。为了使这个定理成立,扰动参数的估计需要以交叉拟合的方式进行(参见 _OrthoLearner)。后一种鲁棒性源于以下事实:与最终最小二乘估计(即平方损失的梯度)相对应的矩方程满足相对于扰动参数 \(q, f\) 的 Neyman 正交条件。有关 Neyman 正交性如何带来鲁棒性的更详细阐述,请参阅 [Chernozhukov2016]、[Mackey2017]、[Nie2017]、[Chernozhukov2017]、[Chernozhukov2018]、[Foster2019]。
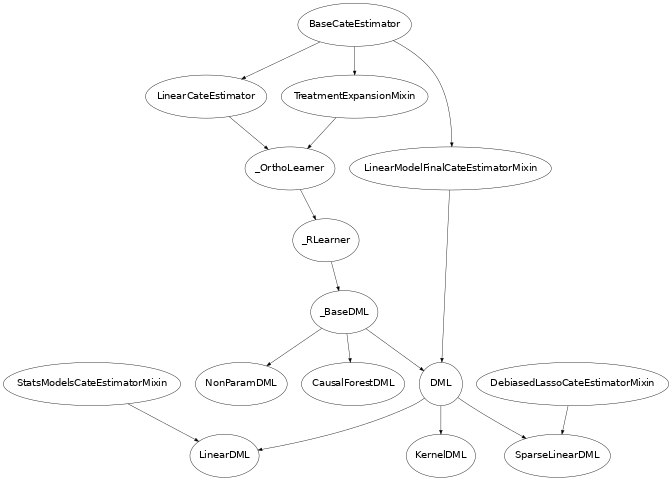
类继承结构
在此库中,我们实现了上一节中提到的几种方法的变体。已实现的 CATE 估计器的继承结构如下。
下面我们简要介绍一下这些类
DML. 类
DML假设每个结果 \(i\) 和处理 \(j\) 的效应模型是线性的,即形式为 \(\theta_{ij}(X)=\langle \theta_{ij}, \phi(X)\rangle\),并允许将任意 scikit-learn 线性估计器定义为最终阶段模型(例如ElasticNet、Lasso、LinearRegression以及在有多个结果(即 \(Y\) 是一个向量)情况下的多任务变体)。最终的线性模型将在由向量 \(T\) 和 \(\phi(X)\) 的 Kronecker 积导出的特征上进行拟合,即 \(\tilde{T}\otimes \phi(X) = \mathtt{vec}(\tilde{T}\cdot \phi(X)^T)\)。这个回归将估计每个结果 \(i\)、处理 \(j\) 和特征 \(k\) 的系数 \(\theta_{ijk}\)。最终模型最小化以下形式的正则化经验平方损失:\[\hat{\Theta} = \arg\min_{\Theta} \E_n\left[ \left(\tilde{Y} - \Theta \cdot \tilde{T}\otimes \phi(X)\right)^2 \right] + \lambda R(\Theta)\]对于某个强凸正则项 \(R\),其中 \(\Theta\) 是参数矩阵,其维度为(结果数,处理数 * 特征数)。例如,如果 \(Y\) 是一维的,并且最后使用的模型是 Lasso,即
from econml.dml import DML from sklearn.linear_model import LassoCV from sklearn.ensemble import GradientBoostingRegressor est = DML(model_y=GradientBoostingRegressor(), model_t=GradientBoostingRegressor(), model_final=LassoCV(fit_intercept=False))则 \(R(\Theta) =\|\Theta\|_1\),如果最后使用的模型是 ElasticNet,即
from econml.dml import DML from sklearn.linear_model import ElasticNetCV from sklearn.ensemble import GradientBoostingRegressor est = DML(model_y=GradientBoostingRegressor(), model_t=GradientBoostingRegressor(), model_final=ElasticNetCV(fit_intercept=False))则 \(R(\Theta)=\kappa \|\Theta\|_2 + (1-\kappa)\|\Theta\|_1\)。对于多维的 \(Y\),可以对参数矩阵 \(\Theta\) 施加几种扩展,例如对应于多任务 Lasso \(\sum_{j} \sum_{i} \theta_{ij}^2\)、多任务 ElasticNet 或核范数正则化 [Jaggi2010],这会在矩阵 \(\Theta\) 上强制执行低秩约束。这本质上实现了在以下文献中分析的技术 [Chernozhukov2016], [Nie2017], [Chernozhukov2017], [Chernozhukov2018]
LinearDML. 子类
LinearDML使用无正则化的最终线性模型,并且基本上只适用于特征向量 \(\phi(X)\) 为低维的情况。由于它是无正则化的低维最终模型,该类还通过渐近正态性论证提供了置信区间。这主要通过使用StatsModelsLinearRegression(它是 scikit-learn LinearRegression 估计器的扩展,也支持推断功能)作为最终模型来实现。该类的理论基础基本上遵循 [Chernozhukov2016] 中的论证。例如,要获取从任何处理 T0 到任何其他处理 T1 的效应的置信区间,只需调用est = LinearDML() est.fit(y, T, X=X, W=W) point = est.effect(X, T0=T0, T1=T1) lb, ub = est.effect_interval(X, T0=T0, T1=T1, alpha=0.05)也可以通过设置 inference='bootstrap' 来构建基于 bootstrap 的置信区间。
SparseLinearDML. 子类
SparseLinearDML使用 \(\ell_1\) 正则化的最终模型。特别是,它使用了 DebiasedLasso 算法 [Buhlmann2011] 的实现(参见DebiasedLasso)。利用去偏 lasso 的渐近正态性性质,该类也提供了基于渐近正态性的置信区间。该类的理论基础基本上遵循 [Chernozhukov2017]、[Chernozhukov2018] 中的论证。例如,要获取从任何处理 T0 到任何其他处理 T1 的效应的置信区间,只需调用from econml.dml import SparseLinearDML est = SparseLinearDML() est.fit(y, T, X=X, W=W) point = est.effect(X, T0=T0, T1=T1) lb, ub = est.effect_interval(X, T0=T0, T1=T1, alpha=0.05)KernelDML. 子类
KernelDML执行了 [Nie2017] 中提出的 RKHS 方法的变体。它通过创建随机傅里叶特征来近似 RKHS 中的任意函数。然后运行 ElasticNet 正则化的最终模型。因此,它通过 RKHS 中函数的随机傅里叶特征近似表示来近似实现 [Nie2017] 的结果。此外,考虑到我们使用了随机傅里叶特征,该类假设使用 RBF 核函数。NonParamDML. 类
NonParamDML对每个结果 \(i\) 的效应模型不作任何假设。然而,它只适用于处理为二元或单维连续的情况。它利用了以下观察结果:对于单维处理,平方损失可以重写为\[\E_n\left[ \left(\tilde{Y} - \theta(X) \cdot \tilde{T}\right)^2 \right] = \E_n\left[ \tilde{T}^2 \left(\frac{\tilde{Y}}{\tilde{T}} - \theta(X)\right)^2 \right]\]后者对应于一个加权回归问题,其中目标标签是 \(\tilde{Y}/\tilde{T}\),特征是 \(X\),每个样本的权重是 \(\tilde{T}^2\)。因此,任何接受样本权重的 scikit-learn 回归器都可以用作最终模型,例如
from econml.dml import NonParamDML from sklearn.ensemble import GradientBoostingRegressor est = NonParamDML(model_y=GradientBoostingRegressor(), model_t=GradientBoostingRegressor(), model_final=GradientBoostingRegressor()) est.fit(y, t, X=X, W=W) point = est.effect(X, T0=t0, T1=t1)示例包括随机森林(
RandomForestRegressor)、梯度提升森林(GradientBoostingRegressor)和支持向量机(SVC)。此外,我们提供了一个包装器WeightedModelWrapper,为任何 scikit-learn 回归器添加样本权重功能。此外,对于特定估计器,我们提供了更定制化的 scikit-learn 扩展,例如WeightedLasso。因此,任何此类模型,甚至执行自动模型选择的交叉验证估计器,都可以用作 model_final。从这个角度来看,这个估计器也是一个 Meta-Learner,因为估计的所有步骤都使用了现成的 ML 算法。欲了解更多信息,请查看 Meta Learners 用户指南。CausalForestDML. 这是
_RLearner的子类,使用 Causal Forest 作为最终模型(参见 [Wager2018] 和 [Athey2019])。Causal Forest 在库中以 scikit-learn 预测器实现,类为CausalForest。此估计器通过 [Athey2019] 中描述的 Bootstrap-of-Little-Bags 方法提供置信区间。利用此功能,我们也可以构建 CATE 的置信区间from econml.dml import CausalForestDML from sklearn.ensemble import GradientBoostingRegressor est = CausalForestDML(model_y=GradientBoostingRegressor(), model_t=GradientBoostingRegressor()) est.fit(y, t, X=X, W=W) point = est.effect(X, T0=t0, T1=t1) lb, ub = est.effect_interval(X, T0=t0, T1=t1, alpha=0.05)请查看 基于森林的估计器用户指南,了解更多关于基于森林的 CATE 模型以及
CausalForestDML的其他替代方案。_RLearner. 内部私有类
_RLearner是DML的父类,允许用户指定任何拟合最终模型的方式,该模型将残差 \(\tilde{T}\) 和特征 \(X\) 作为输入,并预测残差 \(\tilde{Y}\)。此外,扰动参数模型以 \(X\) 和 \(W\) 作为输入,并分别预测 \(T\) 和 \(Y\)。由于这些模型接受非标准输入变量,因此不能将现成的 scikit-learn 估计器用作此类的输入。因此,使用起来稍微繁琐一些,这也是我们将其指定为私有的原因。但是,如果想例如为 \(\theta(X)\) 拟合一个神经网络模型,则可以使用此类(参见DML的实现,了解如何包装 sklearn 估计器并将其作为输入传递给_RLearner)。这个私有类基本上遵循 [Nie2017] 中提出的 RLearner 的一般论证和术语,并允许最终模型估计具有 [Foster2019] 中提出的完全灵活性。
使用常见问题
如果我想要置信区间怎么办?
对于有效的置信区间,如果用于异质性的特征 \(X\) 的数量相对于样本数量较少,则使用
LinearDML。如果特征数量与样本数量相当,则使用SparseLinearDML。例如:from econml.dml import LinearDML est = LinearDML() est.fit(y, T, X=X, W=W) lb, ub = est.const_marginal_effect_interval(X, alpha=.05) lb, ub = est.coef__interval(alpha=.05) lb, ub = est.effect_interval(X, T0=T0, T1=T1, alpha=.05)
如果您有单维连续处理或二元处理,您也可以拟合非线性模型,并通过使用
CausalForestDML来获取置信区间。该类对于高维特征也能很好地工作,只要这些特征中只有少数是真正相关的。为什么不直接用所有处理、特征和控制变量运行一个简单的da型线性回归?
如果您想估计平均处理效应并伴随置信区间,一种可能的方法是简单地运行一个大型线性回归,将 \(Y\) 对 \(T, X, W\) 进行回归,然后查看与 \(T\) 变量相关的系数和相应的置信区间(例如,使用
OLS等统计软件包)。然而,这在以下情况下不起作用:1) 您拥有的控制变量 \(X, W\) 数量很大,与样本数量相当。例如,当需要控制个体固定效应时,控制变量的数量至少等于个体数量,就会出现这种情况。在这种高维设置下,普通最小二乘法 (OLS) 不是一个合理的方法。通常,控制变量的协方差矩阵将是病态的,推断将是无效的。DML 方法通过使用 ML 方法适当正则化估计,并在给定样本数量的情况下提供更好的模型来描述控制变量如何影响结果,从而绕过了这个问题。
2) 变量 \(X, W\) 对结果 \(Y\) 的影响不是线性的。在这种情况下,OLS 将无法提供一致的模型,这可能导致严重的效应估计偏差。DML 方法与非线性第一阶段模型(如随机森林或梯度提升森林)结合使用时,可以捕捉这些非线性,并提供 \(T\) 对 \(Y\) 效应的无偏估计。此外,它这样做的方式对这些 ML 算法可能产生的估计误差具有鲁棒性。
此外,人们通常可能希望估计处理效应的异质性,而上述 OLS 方法无法提供这一点。提供这种异质性的一种可能方法是在 OLS 模型中包含形式为 \(X\cdot T\) 的乘积特征。然而,这样一来又面临与上述相同的问题:
1) 如果效应异质性没有线性形式,那么这种方法是无效的。可能需要创建更复杂的特征化,在这种情况下,问题对于 OLS 来说可能变得过于高维。我们的
SparseLinearDML可以通过使用去偏 Lasso 处理此类设置。我们的CausalForestDML甚至不需要显式特征化,它会自动学习基于森林的非线性 CATE 模型。此外,如果您想要更灵活的 CATE 模型,也可以查看 基于森林的估计器用户指南 和 Meta Learners 用户指南。2) 如果特征 \(X\) 的数量与样本数量相当,即使使用线性模型,OLS 方法也无法可行或统计功效非常小。
如果我不知道异质性是什么样的怎么办?
要么使用灵活的特征化器,例如具有许多阶的多项式特征化器,并使用
SparseLinearDMLfrom econml.dml import SparseLinearDML from sklearn.preprocessing import PolynomialFeatures est = SparseLinearDML(featurizer=PolynomialFeatures(degree=4, include_bias=False)) est.fit(y, T, X=X, W=W) lb, ub = est.const_marginal_effect_interval(X, alpha=.05)
或者,您也可以使用基于森林的估计器,例如
CausalForestDML。该估计器也可以处理许多特征,尽管通常比稀疏线性 DML 处理的特征数量要少。此外,该估计器基本上执行自动特征化,并且可以拟合非线性模型。from econml.dml import CausalForestDML from sklearn.ensemble import GradientBoostingRegressor est = CausalForestDML(model_y=GradientBoostingRegressor(), model_t=GradientBoostingRegressor()) est.fit(y, t, X=X, W=W) lb, ub = est.const_marginal_effect_interval(X, alpha=.05)
此外,还可以查看 正交随机森林用户指南 或 Meta Learners 用户指南。
如果我有太多可能产生异质性的特征怎么办?
使用
SparseLinearDML或CausalForestDML(见上文)。如果我想控制的特征太多怎么办?
使用适用于高维特征的第一阶段模型。例如,Lasso、ElasticNet 或梯度提升森林都是不错的选择(后者允许模型中的非线性,但通常比前者处理的特征数量少),例如:
from econml.dml import SparseLinearDML from sklearn.linear_model import LassoCV, ElasticNetCV from sklearn.ensemble import GradientBoostingRegressor est = SparseLinearDML(model_y=LassoCV(), model_t=LassoCV()) est = SparseLinearDML(model_y=ElasticNetCV(), model_t=ElasticNetCV()) est = SparseLinearDML(model_y=GradientBoostingRegressor(), model_t=GradientBoostingRegressor())
只要这些第一阶段模型实现了较小的均方误差,置信区间仍然有效。
第一阶段估计应该使用什么方法?
参见上文。第一阶段问题是纯粹的预测任务,因此任何与您的预测问题相关的 ML 方法都可以。
如何选择第一阶段模型的超参数?
您可以使用自动选择超参数的交叉验证模型,例如
LassoCV而不是Lasso。类似地,对于基于森林的估计器,您可以使用网格搜索交叉验证器GridSearchCV进行包装,例如:from econml.dml import SparseLinearDML from sklearn.ensemble import RandomForestRegressor from sklearn.model_selection import GridSearchCV first_stage = lambda: GridSearchCV( estimator=RandomForestRegressor(), param_grid={ 'max_depth': [3, None], 'n_estimators': (10, 30, 50, 100, 200), 'max_features': (1,2,3) }, cv=10, n_jobs=-1, scoring='neg_mean_squared_error' ) est = SparseLinearDML(model_y=first_stage(), model_t=first_stage())
或者,您可以在 EconML 框架之外选择最佳的第一阶段模型,并将选定的模型传递给 EconML。这可以节省运行时间和计算资源。此外,这在统计上更稳定,因为所有数据都用于超参数调优,而不是 DML 算法内部的单个折叠(只要您选择的超参数值数量不是样本数量的指数级,这种方法在统计上是有效的)。例如:
from econml.dml import LinearDML from sklearn.ensemble import RandomForestRegressor from sklearn.model_selection import GridSearchCV first_stage = lambda: GridSearchCV( estimator=RandomForestRegressor(), param_grid={ 'max_depth': [3, None], 'n_estimators': (10, 30, 50, 100, 200), 'max_features': (1,2,3) }, cv=10, n_jobs=-1, scoring='neg_mean_squared_error' ) model_y = first_stage().fit(X, Y).best_estimator_ model_t = first_stage().fit(X, T).best_estimator_ est = LinearDML(model_y=model_y, model_t=model_t)
如何选择最终模型(如果存在)的超参数?
您也可以为最终模型使用交叉验证类。我们的默认去偏 lasso 会对超参数进行交叉验证选择。对于自定义最终模型,您也可以使用 CV 版本,例如:
from econml.dml import DML from sklearn.linear_model import ElasticNetCV from sklearn.ensemble import GradientBoostingRegressor est = DML(model_y=GradientBoostingRegressor(), model_t=GradientBoostingRegressor(), model_final=ElasticNetCV(fit_intercept=False)) est.fit(y, t, X=X, W=W) point = est.const_marginal_effect(X) point = est.effect(X, T0=t0, T1=t1)
在使用
NonParamDML的情况下,您也可以使用非线性交叉验证模型作为 model_finalfrom econml.dml import NonParamDML from sklearn.ensemble import RandomForestRegressor from sklearn.model_selection import GridSearchCV cv_reg = lambda: GridSearchCV( estimator=RandomForestRegressor(), param_grid={ 'max_depth': [3, None], 'n_estimators': (10, 30, 50, 100, 200, 400, 600, 800, 1000), 'max_features': (1,2,3) }, cv=10, n_jobs=-1, scoring='neg_mean_squared_error' ) est = NonParamDML(model_y=cv_reg(), model_t=cv_reg(), model_final=cv_reg())
如果我有许多处理怎么办?
该方法将假设每个处理都以线性方式进入模型。因此,它无法捕捉不同处理之间的互补性或替代性。为此,您也可以创建复合处理,例如两个基本处理的乘积。然后这些乘积将进入模型,并估计该乘积的效应。这个效应将是同时存在两个处理时的替代/互补效应。请参见下文以获取更多示例。
如果处理数量太多,则可以使用
SparseLinearDML。然而,该方法本质上会施加正则化,使得只有您特征化处理的一小部分产生效应。如果我的处理是连续的并且对结果没有线性效应怎么办?
您可以通过为估计器指定 treatment_featurizer 来施加特定的非线性形式。例如,可以使用 sklearn 的 PolynomialFeatures 转换器作为 treatment_featurizer 来学习高阶多项式处理效应。
使用 treatment_featurizer 参数还有一个额外的好处,即能够计算相对于原始处理维度的边际效应,而不是在传递给估计器之前自行对处理进行特征化。
from econml.dml import LinearDML from sklearn.preprocessing import PolynomialFeatures poly = PolynomialFeatures(degree=2, interaction_only=True, include_bias=False) est = LinearDML(treatment_featurizer=poly) est.fit(y, T, X=X, W=W) point = est.const_marginal_effect(X) est.effect(X, T0=T0, T1=T1) est.marginal_effect(T, X)
或者,您仍然可以创建复合处理并将它们作为额外的处理变量添加
from econml.dml import LinearDML from sklearn.preprocessing import PolynomialFeatures poly = PolynomialFeatures(degree=2, interaction_only=True, include_bias=False) est = LinearDML() T_composite = poly.fit_transform(T) est.fit(y, T_composite, X=X, W=W) point = est.const_marginal_effect(X) est.effect(X, T0=poly.transform(T0), T1=poly.transform(T1))
如果我的处理是分类/二元的怎么办?
您只需在类的参数中设置 discrete_treatment=True。然后为 model_t 使用任何具有 predict_proba 方法的分类器
from econml.dml import LinearDML from sklearn.linear_model import LogisticRegressionCV est = LinearDML(model_t=LogisticRegressionCV(), discrete_treatment=True) est.fit(y, t, X=X, W=W) point = est.const_marginal_effect(X) est.effect(X, T0=t0, T1=t1)
如何评估 CATE 模型的性能?
每个 DML 类拟合后都有一个属性 score_。因此,可以访问该属性并比较不同建模参数下的性能(分数越低越好)
from econml.dml import DML from sklearn.linear_model import ElasticNetCV from sklearn.ensemble import RandomForestRegressor est = DML(model_y=RandomForestRegressor(), model_t=RandomForestRegressor(), model_final=ElasticNetCV(fit_intercept=False), featurizer=PolynomialFeatures(degree=1)) est.fit(y, T, X=X, W=W) est.score_
这基本上衡量了基于最终阶段损失的分数。此外,可以通过在未用于训练的单独验证样本上调用 score 方法来评估样本外分数
est.score(Y_val, T_val, X_val, W_val)
此外,可以通过检查已拟合模型来独立检查已拟合的第一阶段模型的拟合优度。您可以通过方法 models_t 和 models_y 访问已拟合的第一阶段模型的嵌套列表(交叉拟合结构的每个折叠都有一个)。如果这些模型也具有相关的评分属性,则可以将其用作第一阶段性能的指标。例如,在上述随机森林作为第一阶段模型的情况下,如果 oob_score 设置为 True,则估计器具有拟合后的性能度量
[mdl.oob_score_ for mdls in est.models_y for mdl in mdls]
如果使用交叉验证估计器作为第一阶段模型,则会自动执行第一阶段模型的模型选择。
如何设置参数 cv?
此参数定义了创建的数据分区数量,以便以交叉拟合的方式拟合第一阶段(参见
_OrthoLearner)。默认值为 2,这是最小值。然而,更大的值,如 5 或 6,可以提高方法的统计稳定性,特别是在样本数量较少的情况下。因此,我们建议对于小型数据集,应增加此值。这可能会增加计算成本,因为需要拟合更多第一阶段模型。
使用示例
有关更广泛的示例,请查看以下 notebooks:DML 示例 Jupyter Notebook,森林学习器 Jupyter Notebook。
单结果,单处理
我们考虑该库在 \(Y\) 和 \(T\) 为 1 维时的一些使用示例。
随机森林第一阶段. 第一阶段估计的经典非参数回归器是随机森林。在我们的 API 中使用 RandomForests 非常简单,如下所示:
from econml.dml import LinearDML
from sklearn.ensemble import RandomForestRegressor
est = LinearDML(model_y=RandomForestRegressor(),
model_t=RandomForestRegressor())
est.fit(y, T, X=X, W=W)
pnt_effect = est.const_marginal_effect(X)
lb_effect, ub_effect = est.const_marginal_effect_interval(X, alpha=.05)
pnt_coef = est.coef_
lb_coef, ub_coef = est.coef__interval(alpha=.05)
用于异质性的多项式特征. 假设我们认为处理效应是 \(X\) 的多项式,即:
然后我们可以通过运行以下代码估计系数 \(\alpha_i\)
from econml.dml import LinearDML
from sklearn.ensemble import RandomForestRegressor
from sklearn.preprocessing import PolynomialFeatures
est = LinearDML(model_y=RandomForestRegressor(),
model_t=RandomForestRegressor(),
featurizer=PolynomialFeatures(degree=3, include_bias=True))
est.fit(y, T, X=X, W=W)
# To get the coefficients of the polynomial fitted in the final stage we can
# access the `coef_` attribute of the fitted second stage model. This would
# return the coefficients in front of each term in the vector T⊗ϕ(X).
est.coef_
固定效应. 要添加固定效应异质性,我们可以创建 id 的独热编码,id 假设是输入的一部分
from econml.dml import LinearDML
from sklearn.preprocessing import OneHotEncoder
# removing one id to avoid colinearity, as is standard for fixed effects
X_oh = OneHotEncoder(sparse_output=False).fit_transform(X)[:, 1:]
est = LinearDML(model_y=RandomForestRegressor(),
model_t=RandomForestRegressor())
est.fit(y, T, X=X_oh, W=W)
# The latter will fit a model for θ(x) of the form ̂α_0 + ̂α_1 𝟙{id=1} + ̂α_2 𝟙{id=2} + ...
# The vector of α can be extracted as follows
est.coef_
自定义特征. 只要自定义特征化器支持 sklearn 的 fit_transform 接口,就可以定义它。
from sklearn.ensemble import RandomForestRegressor
class LogFeatures(object):
"""Augments the features with logarithmic features and returns the augmented structure"""
def fit(self, X, y=None):
return self
def transform(self, X):
return np.concatenate((X, np.log(1+X)), axis=1)
def fit_transform(self, X, y=None):
return self.fit(X).transform(X)
est = LinearDML(model_y=RandomForestRegressor(),
model_t=RandomForestRegressor(),
featurizer=LogFeatures())
est.fit(y, T, X=X, W=W)
我们甚至可以创建一个特征化器的 Pipeline 或 Union,它将应用多种特征化,例如先创建对数特征,然后添加它们的多项式
from econml.dml import LinearDML
from sklearn.ensemble import RandomForestRegressor
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
est = LinearDML(model_y=RandomForestRegressor(),
model_t=RandomForestRegressor(),
featurizer=Pipeline([('log', LogFeatures()),
('poly', PolynomialFeatures(degree=2))]))
est.fit(y, T, X=X, W=W)
单结果,多处理
假设我们要同时估计多个连续处理的处理效应。然后我们可以简单地在将它们传递给估计器之前将它们连接起来。
import numpy as np
est = LinearDML()
est.fit(y, np.concatenate((T0, T1), axis=1), X=X, W=W)
多结果,多处理
在需求估计等场景中,我们可能希望将多种产品的需求拟合为各自价格的函数,即拟合交叉价格弹性矩阵。这可以通过简单地将 \(Y\) 设置为需求向量,将 \(T\) 设置为价格向量来实现。然后我们可以恢复交叉价格弹性矩阵,如下所示:
from sklearn.linear_model import MultiTaskElasticNet
est = LinearDML(model_y=MultiTaskElasticNet(alpha=0.1),
model_t=MultiTaskElasticNet(alpha=0.1))
est.fit(Y, T, X=None, W=W)
# a_hat[i,j] contains the elasticity of the demand of product i on the price of product j
a_hat = est.const_marginal_effect()
如果产品过多,交叉价格弹性矩阵包含许多参数,我们需要进行正则化。考虑到我们希望估计一个矩阵,在此应用中考虑该矩阵具有低秩的情况是合理的:所有产品都可以嵌入到某个低维特征空间中,而交叉价格弹性是这些低维嵌入的线性函数。这对应于定价中研究深入的隐因子模型。我们的框架可以通过在最终阶段使用核范数正则化的多任务回归轻松处理这种情况。例如,lightning 包实现了这样一个类
from econml.dml import DML
from sklearn.preprocessing import PolynomialFeatures
from lightning.regression import FistaRegressor
from sklearn.linear_model import MultiTaskElasticNet
est = DML(model_y=MultiTaskElasticNet(alpha=0.1),
model_t=MultiTaskElasticNet(alpha=0.1),
model_final=FistaRegressor(penalty='trace', C=0.0001),
fit_cate_intercept=False)
est.fit(Y, T, X=X, W=W)
te_pred = est.const_marginal_effect(np.median(X, axis=0, keepdims=True))
print(te_pred)
print(np.linalg.svd(te_pred[0]))