基于森林的估计器

它是什么？

本节介绍了包中提供的不同估计方法，这些方法使用基于森林的方法来建模处理效应的异质性。我们将这些方法收集在一个用户指南中，以便更好地说明它们的比较和区别。目前，我们的包提供了三种这样的估计方法：

• 正交随机森林估计器（参见 DMLOrthoForest, DROrthoForest）

• 森林双重机器学习估计器（又称因果森林）（参见 CausalForestDML）

• 森林双重鲁棒估计器（参见 ForestDRLearner）。

这些估计器与 DML 和 DR 部分类似，都需要无混淆假设，即所有可能同时影响处理和结果的潜在变量都必须被观察到。

这些估计器之间有许多共同点。特别是 DMLOrthoForest 与 CausalForestDML 有很多相似之处，而 DROrthoForest 与 ForestDRLearner 有很多相似之处。具体来说，对应的类使用相同的估计（矩）方程来识别异质处理效应。然而，它们在如何估计第一阶段回归/分类（混杂）模型方面存在显著差异。特别是，OrthoForest 方法围绕目标特征 \(X\) 拟合局部混杂参数，从而优化局部均方误差，对在 \(X\) 空间中看起来相似的样本赋予更多权重。相似性度量由一种数据自适应的基于森林的方法捕获，该方法试图在 \(X\) 空间中学习一个度量，使得相似的点具有相似的处理效应。相反，DML 和 DR 森林方法执行全局第一阶段拟合，这通常会优化整体均方误差。局部拟合在很多时候可以提高 CATE 估计的最终性能。然而，它确实会增加一些额外的计算成本，因为每个目标预测点都需要拟合单独的第一阶段模型。这三种方法都能提供有效的置信区间，因为它们的估计值是渐近正态的。此外，这些方法在有限样本中定义相似性度量的方式略有不同，OrthoForest 试图构建一个森林来定义相似性度量，该度量在内部执行节点上的混杂估计，并将相同的度量用于混杂的局部拟合以及最终的 CATE 估计。有关这些方法的更多技术细节，请参阅 [Wager2018]、[Athey2019]、[Oprescu2019]。

相关的估计器类有哪些？

本节描述了类 DMLOrthoForest、DROrthoForest、CausalForestDML、ForestDRLearner 中实现的方法论。点击这些链接中的每一个，可查看每个类的详细模块文档和输入参数。

何时应该使用它？

这些方法可以估计异质处理效应的非常灵活的非线性模型。此外，它们是数据自适应方法，并适应数据生成过程的低维潜在结构。因此，即使有许多特征，它们也能表现良好，尽管它们执行的是非参数估计（这通常需要相对于样本数量较少的特征）。最后，尽管这些方法是数据自适应和非参数的，但它们利用了文献中的最新思想，以提供有效的置信区间。因此，如果您有许多特征，对您的效应异质性如何表现没有好的想法，并且希望获得置信区间，那么您应该使用这些方法。

正式方法论概述

正交随机森林

正交随机森林 [Oprescu2019] 是因果森林和双重机器学习的结合，它允许控制高维混杂因素 \(W\)，同时在较低维变量集 \(X\) 上非参数地估计异质处理效应 \(\theta(X)\)。此外，估计值是渐近正态的，因此具有理论性质，使得基于自助法的置信区间渐近有效。

对于连续或离散处理（参见 DMLOrthoForest），该方法通过求解与双重机器学习框架中使用的相同的矩方程组来估计某个目标 \(x\) 的 \(\theta(x)\)，尽管它试图为每一个可能的 \(X=x\) 局部地求解它们。该方法对数据生成过程作出以下结构方程假设：

\[\begin{split}Y =~& \theta(X) \cdot T + g(X, W) + \epsilon ~~~&~~~ \E[\epsilon | X, W] = 0 \\ T =~& f(X, W) + \eta & \E[\eta \mid X, W] = 0 \\ ~& \E[\eta \cdot \epsilon | X, W] = 0\end{split}\]

但不对函数 \(\theta, g, f\) 作出进一步的强假设。它主要假设 \(\theta\) 是一个 Lipschitz 函数。它通过局部矩条件集来识别函数 \(\theta\)：

\[\E[\left( Y - \E[Y \mid X, W] - \theta(x)\cdot (T- \E[T \mid X, W]) \right)\cdot \left(T - \E[T \mid X, W]\right) \mid X=x]=0\]

等价地，如果我们令 \(q(X, W)=\E[Y | X, W]\)，那么我们可以将后者重写为：

\[\E[\left( Y - q(x, W) - \theta(x) \cdot (T- f(X, W)) \rangle \right)\cdot \left(T - f(X, W)\right) \mid X=x]=0\]

这是 DML 损失的局部版本，因为上述等价于在 \(X=x\) 点局部地最小化残差 \(Y\) 对残差 \(T\) 的平方损失：

\[\theta(x) = \argmin_{\theta} \E[\left( Y - q(X, W) - \theta \cdot (T- f(X, W)) \right)^2 \mid X=x]\]

当采用这种识别方法进行估计时，我们将用局部加权的经验平均值替换局部矩方程，并用这些条件期望的局部估计值 \(\hat{q}_x(X, W)\), \(\hat{f}_x(X, W)\) 替换函数 \(q(X, W)\), \(f(X, W)\)（这些通常在 \(x\) 附近是参数/线性函数）。

\[\sum_{i=1}^n K_x(X_i)\cdot \left( Y_i - \hat{q}_x(X_i, W_i) - \hat{\theta}(x) \cdot (T_i - \hat{f}_x(X_i, W_i)) \right)\cdot \left(T_i - \hat{f}_x(X_i, W_i)\right) = 0\]

或者等价地最小化局部平方损失（即运行局部线性回归）

\[\hat{\theta}(x) = \argmin_{\theta} \sum_{i=1}^n K_x(X_i)\cdot \left( Y_i - \hat{q}_x(X_i, W_i) - \theta \cdot (T_i - \hat{f}_x(X_i, W_i)) \right)^2\]

事实上，在我们的包中，我们还实现了 [Friedberg2018] 中提出的局部线性修正，即不是在局部拟合一个常数 \({\theta}\)，而是在局部拟合一个 \(X\) 的线性函数并对线性部分进行正则化，即：

\[\begin{split}\hat{\alpha}, \hat{\beta} =~& \argmin_{\alpha, \beta} \sum_{i=1}^n K_x(X_i) \left( Y_i - \hat{q}_x(X_i, W_i) - (\beta\cdot X_i + \alpha) (T_i - \hat{f}_x(X_i, W_i)) \right)^2 + \lambda \|\beta\|_2^2\\ \hat{\theta}(x) =~& \hat{\beta} \cdot x + \hat{\alpha}\end{split}\]

核函数 \(K_x(X_i)\) 是一个通过构建具有因果准则的随机森林计算得到的相似性度量。该准则是在广义随机森林 [Athey2019] 和因果森林 [Wager2018] 中使用的准则的轻微修改，以便在计算每个候选分割的分数时纳入残差化。

此外，对于每个目标点 \(x\)，我们将需要估计函数 \(q(X, W) = \E[Y | X, W]\) 和 \(f(X, W)=\E[T | X, W]\) 的局部混杂函数 \({\hat{q}_x(X, W)}\), \({\hat{f}_x(X, W)}\)。该方法分割数据并执行交叉拟合：即在前一半数据上拟合条件期望模型，然后在后一半数据上预测这些量，反之亦然。随后在所有数据上估计 \({\theta(x)}\)。

为了处理高维 \(W\)，该方法还在每个目标 \(x\) 周围以局部方式估计条件期望。特别是，对于每个目标 \(x\)，为了估计 \({\hat{q}_x(X, W)}\), \({\hat{f}_x(X, W)}\)，它最小化一个加权（惩罚）损失 \({\ell}\)（例如平方损失或多项逻辑损失）

\[\begin{split}\hat{q}_x = \argmin_{q_x \in Q} \sum_{i=1}^n K_x(X_i)\cdot \ell(Y_i, q_x(X_i, W_i)) + R(q_x)\\ \hat{f}_x = \argmin_{f_x \in F} \sum_{i=1}^n K_x(X_i)\cdot \ell(T_i, f_x(X_i, W_i)) + R(f_x)\end{split}\]

其中 \(Q, F\) 是某些函数空间，\(R\) 是某些正则项。如果假设空间是局部线性的，即 \(h_x(X, W) = \langle \nu(x), [X; W] \rangle\)，正则项是系数的 \(\ell_1\) 范数 \(\|\nu(x)\|_1\)，损失是平方损失或逻辑损失，那么该方法具有渐近正态性的可证明保证，假设真实系数相对稀疏（即大多数为零）。权重 \(K(x, X_i)\) 使用具有因果准则的相同随机森林算法计算，与计算 \({\theta(x)}\) 第二阶段估计权重的算法相同（尽管在交叉拟合方式下使用了与最终阶段估计不同的半样本）。

算法上，该方法的混杂估计部分以灵活的方式实现，不限于 \({\ell_1}\) 正则化，具体如下：用户可以定义任何支持 fit 和 predict 的类。fit 函数还需要支持样本权重，作为第三个参数传递。如果不支持，我们提供了一个加权模型包装器 WeightedModelWrapper，它可以包装任何支持 fit 和 predict 的类，并启用样本权重功能。此外，我们还提供了 scikit-learn 库的一些扩展，以支持样本权重，例如 WeightedLasso。

>>> est = DMLOrthoForest(model_Y=WeightedLasso(), model_T=WeightedLasso())

对于离散处理（参见 DROrthoForest），该方法通过求解一组略有不同的方程来估计某个目标 \(x\) 的 \({\theta(x)}\)，类似于双重鲁棒学习器（参见 [Oprescu2019]，其中有关于为何使用不同估计方程组的理论阐述）。特别是，假设处理 \(T\) 取值于 \(\{0, 1, \ldots, k\}\)，那么为了估计处理 \(t\) 相较于处理 \(0\) 的处理效应 \({\theta_t(x)}\)，该方法找到方程的解：

\[\E\left[ Y_{i,t}^{DR} - Y_{i,0}^{DR}- \theta_t(x) | X=x\right] = 0\]

其中 \(Y_{i,t}^{DR}\) 是基于双重鲁棒的样本 \(i\) 接受处理 \(t\) 时的反事实结果的无偏估计，即：

\[Y_{i,t}^{DR} = \E[Y \mid T=t, X_i, W_i] + 1\{T_i=t\} \frac{Y_i - \E[Y \mid T=t, X_i, W_i]}{\E[1\{T=t\} \mid X_i, W_i]}\]

等价地，我们可以将其表示为最小化局部平方损失：

\[\theta_t(x) = \argmin_{\theta_t} \E\left[(Y_{i,t}^{DR} - Y_{i,0}^{DR}- \theta_t)^2 | X=x\right]\]

类似于连续处理情况，我们通过最小化局部加权平方损失并将局部线性校正应用于估计，从而将此识别策略转化为估计方法。

\[\begin{split}\hat{\alpha}_t, \hat{\beta}_t =& \argmin_{\alpha_t, \beta_t} \sum_{i=1}^n K(x, X_i)\cdot \left( Y_{i,t}^{DR} - Y_{i,0}^{DR}- \beta_t\cdot X_i + \alpha_t \right)^2 + \lambda \|\beta_t\|_2^2\\ \hat{\theta}_t(x) =& \hat{\beta}_t \cdot x + \hat{\alpha}_t\end{split}\]

其中，在构建双重鲁棒估计时，我们使用条件期望 \({\E[Y \mid T=t, X, W]}\) 和 \({\E[1\{T=t\} \mid X, W]}\) 的第一阶段局部估计值 \(g_x(T, X, W)\), \(p_{x, t}(X, W)\)。这些通过交叉拟合方式，相应地拟合局部加权回归和分类模型来估计。我们注意到，在离散处理的情况下，处理的模型是多类别分类模型，并且应该支持 predict_proba。

有关正交森林类的输入参数以及如何自定义估计器的更多详细信息，请查阅这两个模块：

• DROrthoForest

• DMLOrthoForest

因果森林（又称森林双重机器学习）

在本包中，我们实现了因果森林/广义随机森林的双重机器学习版本（参见 [Wager2018], [Athey2019]），例如在 [Athey2019] 的第 6.1.1 节中描述的那样。这个版本遵循与 DMLOrthoForest 方法类似的结构，即估计基于求解一个局部残差对残差的矩条件：

\[\hat{\theta}(x) = \argmin_{\theta} \sum_{i=1}^n K_x(X_i)\cdot \left( Y_i - \hat{q}(X_i, W_i) - \theta \cdot (T_i - \hat{f}(X_i, W_i)) \right)^2\]

相似性度量 \(K_x(X_i)\) 通过构建一个具有因果准则的二次抽样 Honest 随机森林来以数据自适应的方式训练，并粗略计算样本 \(x\) 与样本 \(X_i\) 落入同一叶子的频率。

因果森林与 OrthoForest 有两个主要区别：首先，混杂估计 \({\hat{q}}\) 和 \({\hat{f}}\) 是基于全局目标拟合的，而不是针对每个目标点局部拟合的。因此，它们通常不会最小化某种形式的局部均方误差。其次，可能用于拟合这些估计值（例如如果使用了 RandomForest）的相似性度量与最终效应估计中使用的相似性度量不耦合。这种差异可能导致 OrthoForest 相较于因果森林的估计误差有所改善。然而，它确实增加了显著的计算成本，因为每个目标预测都需要局部估计一个混杂函数。

我们的因果森林实现允许任意数量的连续处理或多值离散处理。因果森林在 CausalForest 中作为 scikit-learn 预测器以高性能 Cython 实现。

除了 [Athey2019] 中提出的准则外，我们还实现了一个 MSE 准则，该准则惩罚处理方差低的分割。这种差异可能导致小的有限样本差异。特别是，假设我们想决定如何将一个节点分割成两个样本子集 \(S_1\) 和 \(S_2\)，并且让 \({\theta_1}\) 和 \({\theta_2}\) 分别是这两个划分上的估计值。那么简化中隐含的准则是加权均方误差，它归结为：

\[\max_{S_1, S_2} \theta_1^2 \sum_{i\in S_1} \tilde{T}_i^2 + \theta_2^2 \sum_{i \in S_2} \tilde{T}_i^2 \approx \max_{S_1, S_2} \theta_1^2 \cdot |S_1| \cdot Var_n(T | x\in S_1) + \theta_2^2 \cdot |S_2|\cdot Var_n(T | x \in S_2)\]

其中 \(Var_n\) 表示经验方差。本质上，该准则试图最大化异质性（通过最大化两个估计值的平方和来捕捉），同时惩罚那些创建处理变异性小的节点的分割。相反，[Athey2019] 中提出的准则忽略了子节点内部处理的变异性，仅最大化异质性，即：

\[\max_{S_1, S_2} \theta_1^2 + \theta_2^2\]

有关双重机器学习以及 CausalForestDML 如何融入我们基于 DML 的 CATE 估计器总体集的更多详细信息，请查阅双重机器学习用户指南。

森林双重鲁棒学习器

森林双重鲁棒学习器是广义随机森林和正交随机森林的一种变体（参见 [Wager2018], [Athey2019], [Oprescu2019]），它使用双重鲁棒矩进行估计，而不是双重机器学习矩（参见双重鲁棒学习用户指南）。该方法仅适用于分类处理。

本质上，它是 DROrthoForest 的一个对应变体，它不进行局部混杂估计，而是进行全局混杂估计，并且不将用于混杂估计的隐式相似性度量与最终阶段的相似性度量耦合。

更具体地说，该方法通过求解局部回归来估计与处理 \(t\) 相关的 CATE：

\[\theta_t(x) = \argmin_{\theta_t} \sum_{i=1}^n K(x, X_i)\cdot \left( Y_{i,t}^{DR} - Y_{i,0}^{DR} - \theta_t \right)^2\]

其中

\[Y_{i,t}^{DR} = \hat{g}(t, X_i, W_i) + 1\{T_i=t\} \frac{Y_i - \hat{g}(t, X_i, W_i)}{\hat{p}_t(X_i, W_i)]}\]

其中 \({\hat{g}(t, X, W)}\) 是 \({\E[Y | T=t, X, W]}\) 的估计值，\({\hat{p}_t(X, W)}\) 是 \({\Pr[T=t | X, W]}\) 的估计值。这些估计在第一阶段估计中以交叉拟合方式构建（有关交叉拟合的更多详细信息，请参见例如 _OrthoLearner）。

相似性度量 \(K_x(X_i)\) 通过构建一个二次抽样 Honest 随机回归森林来以数据自适应的方式训练，其中目标标签是 \(Y_{i, t}^{DR} - Y_{i, 0}^{DR}\)，特征是 \(X\)，并粗略计算样本 \(x\) 与样本 \(X_i\) 落入同一叶子的频率。这在 RegressionForest 中实现（参见 RegressionForest）。

类层次结构

使用示例

这是一个关于如何在简单数据生成过程中调用 DMLOrthoForest 以及返回值的含义的简单示例。更多示例请查看我们的 OrthoForest Jupyter notebook 和 ForestLearners Jupyter notebook。

import numpy as np
import sklearn
from econml.orf import DMLOrthoForest, DROrthoForest
np.random.seed(123)

>>> T = np.array([0, 1]*60)
>>> W = np.array([0, 1, 1, 0]*30).reshape(-1, 1)
>>> Y = (.2 * W[:, 0] + 1) * T + .5
>>> est = DMLOrthoForest(n_trees=1, max_depth=1, subsample_ratio=1,
...                      model_T=sklearn.linear_model.LinearRegression(),
...                      model_Y=sklearn.linear_model.LinearRegression())
>>> est.fit(Y, T, X=W, W=W)
<econml.orf._ortho_forest.DMLOrthoForest object at 0x...>
>>> print(est.effect(W[:2]))
[1.00...  1.19...]

类似地，我们可以调用 DROrthoForest

>>> T = np.array([0, 1]*60)
>>> W = np.array([0, 1, 1, 0]*30).reshape(-1, 1)
>>> Y = (.2 * W[:, 0] + 1) * T + .5
>>> est = DROrthoForest(n_trees=1, max_depth=1, subsample_ratio=1,
...                     propensity_model=sklearn.linear_model.LogisticRegression(),
...                     model_Y=sklearn.linear_model.LinearRegression())
>>> est.fit(Y, T, X=W, W=W)
<econml.orf._ortho_forest.DROrthoForest object at 0x...>
>>> print(est.effect(W[:2]))
[0.99...  1.35...]

现在我们来看一个更复杂的示例，其中包含高维混杂因素 \(W\) 和更真实的噪声数据。在这种情况下，我们可以直接使用类的默认参数，对于连续处理，默认参数指定在处理和结果回归中均使用 LassoCV。

>>> from econml.orf import DMLOrthoForest
>>> from econml.orf import DMLOrthoForest
>>> from econml.sklearn_extensions.linear_model import WeightedLasso
>>> import matplotlib.pyplot as plt
>>> np.random.seed(123)
>>> X = np.random.uniform(-1, 1, size=(4000, 1))
>>> W = np.random.normal(size=(4000, 50))
>>> support = np.random.choice(50, 4, replace=False)
>>> T = np.dot(W[:, support], np.random.normal(size=4)) + np.random.normal(size=4000)
>>> Y = np.exp(2*X[:, 0]) * T + np.dot(W[:, support], np.random.normal(size=4)) + .5
>>> est = DMLOrthoForest(n_trees=100,
...                      max_depth=5,
...                      model_Y=WeightedLasso(alpha=0.01),
...                      model_T=WeightedLasso(alpha=0.01))
>>> est.fit(Y, T, X=X, W=W)
<econml.orf._ortho_forest.DMLOrthoForest object at 0x...>
>>> X_test = np.linspace(-1, 1, 30).reshape(-1, 1)
>>> treatment_effects = est.effect(X_test)
>>> plt.plot(X_test[:, 0], treatment_effects, label='ORF estimate')
[<matplotlib.lines.Line2D object at 0x...>]
>>> plt.plot(X_test[:, 0], np.exp(2*X_test[:, 0]), 'b--', label='True effect')
[<matplotlib.lines.Line2D object at 0x...>]
>>> plt.legend()
<matplotlib.legend.Legend object at 0x...>
>>> plt.show(block=False)

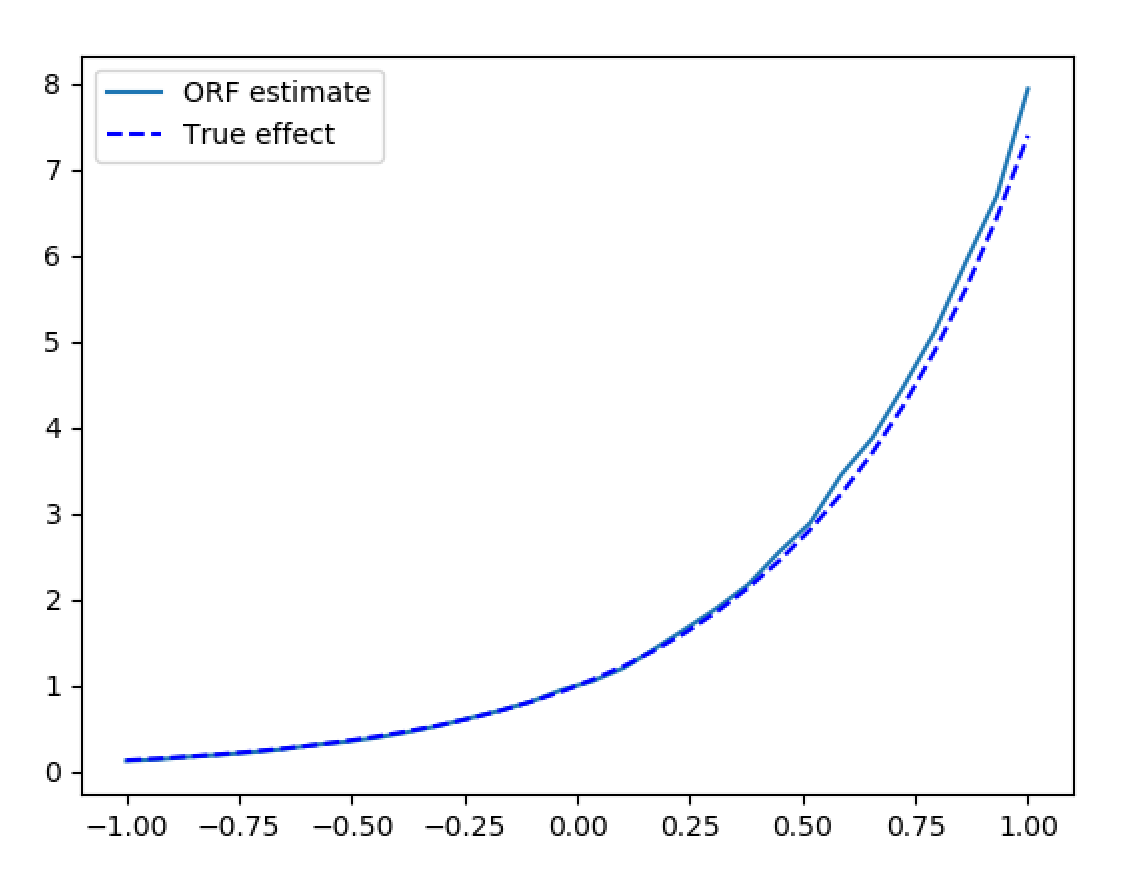
高维控制变量下的合成数据估计