元学习器

这是什么？

元学习器是离散处理 CATE 估计器，它们分别对两个响应曲面 \(Y(0)\) 和 \(Y(1)\)，或多个响应曲面 \(Y(0)\) 到 \(Y(K)\) 进行建模。有关这些方法的详细概述，请参阅 [Kunzel2017]。我们还在更一般的层面上描述了我们的所有估计器类，其中每个估计阶段都可以是任意的 ML 方法（例如 DRLearner 和 NonParamDML）。此外，我们还引入了一种新的元学习器，它使用了机器学习中领域适应的思想（DomainAdaptationLearner）。这些方法属于元学习器类别，因为它们只是以黑箱方式组合了 ML 方法以获得最终阶段的估计，并且没有引入新的估计组件。

有关如何使用我们实现的元学习器的示例，请查看此 元学习器 Jupyter notebook。此处的示例和文档仅基于二元处理设置，但所有这些估计器也适用于多处理设置。

相关的估计器类有哪些？

本节描述了类 SLearner、TLearner、XLearner、DomainAdaptationLearner、NonParamDML、DRLearner 中实现的方法。点击这些链接查看每个类的详细模块文档和输入参数。

何时使用它？

当希望在每个阶段使用何种估计方法具有完全灵活性时，这些方法特别有价值。此外，它们允许用户进行交叉验证，以便在每个阶段进行更多数据自适应的估计。因此，它们允许用户对干扰量和最终的 CATE 模型进行模型选择。然而，由于其不受限制的灵活性，它们通常不提供有效的置信区间，因为尚不清楚任意 ML 方法如何权衡偏差和方差。因此，主要应在目标是估计具有小均方误差的 CATE 并通过交叉验证的估计器执行自动模型选择时使用这些方法。

正式方法论概述

我们在此介绍每个估计器在二元处理情况下的推理。我们的包甚至适用于多个类别处理，并且每种方法都可以自然地扩展到多处理情况，为简洁起见此处省略。

T-学习器

T-学习器分别对 \(Y(0)\) 和 \(Y(1)\) 进行建模。估计的 CATE 由下式给出

\[\begin{split}\hat{\tau}(x) & = E[Y(1)-Y(0)\mid X=x] \\ & = E[Y(1)\mid X=x] - E[Y(0)\mid X=x] \\ & = \hat{\mu}_1(x) - \hat{\mu}_0(x)\end{split}\]

其中 \(\hat{\mu}_0 = M_0(Y^0\sim X^0),\; \hat{\mu}_1 = M_1(Y^1\sim X^1)\) 分别是对照组和处理组的结果模型。这里，\(M_0\) 和 \(M_1\) 可以是任何合适的机器学习算法，它们可以学习特征和结果之间的关系。

EconML 包提供了以下 T-学习器实现：TLearner

S-学习器

S-学习器通过一个将处理分配 \(T\) 作为输入特征（以及特征 \(X\)）的模型来对 \(Y(0)\) 和 \(Y(1)\) 进行建模。估计的 CATE 由下式给出

\[\begin{split}\hat{\tau}(x) & = E[Y \mid X=x, T=1] - E[Y\mid X=x, T=0] \\ & = \hat{\mu}(x, 1) - \hat{\mu}(x, 0)\end{split}\]

其中 \(\hat{\mu}=M(Y \sim (X, T))\) 是针对特征 \(X, T\) 的结果模型。这里，\(M\) 是任何合适的机器学习算法。

EconML 包提供了以下 S-学习器实现：SLearner

X-学习器

X-学习器分别对 \(Y(1)\) 和 \(Y(0)\) 进行建模，以估计 CATT（处理组条件平均处理效应）和 CATC（对照组条件平均处理效应）。新点 \(x\) 的 CATE 估计值由 CATT 和 CATC 的倾向加权平均值给出。下面是 X-学习器过程的概述

\[\begin{split}\hat{\mu}_0 & = M_1(Y^0 \sim X^0) \\ \hat{\mu}_1 & = M_2(Y^1 \sim X^1) \\ \hat{D}^1 & = Y^1 - \hat{\mu}_0(X^1) \\ \hat{D}^0 & = \hat{\mu}_1(X^0) - Y^0 \\ \hat{\tau}_0 & = M_3(\hat{D}^0 \sim X^0) \\ \hat{\tau}_1 & = M_4(\hat{D}^1 \sim X^1) \\ \hat{\tau} & = g(x)\hat{\tau}_0(x) + (1-g(x)) \hat{\tau}_1(x)\end{split}\]

其中 \(g(x)\) 是对 \(P[T=1| X]\) 的估计，\(M_1, M_2, M_3, M_4\) 是合适的机器学习算法。

EconML 包提供了以下 X-学习器实现：XLearner

领域适应学习器

领域适应学习器是 \(X\)-学习器的一种变体，它使用领域适应技术来估计结果模型 \(\hat{\mu}_0\) 和 \(\hat{\mu}_1\)。领域适应方法的基本假设是概率分布 \(P(X^0)\) 和 \(P(X^1)\) 不同。这需要根据 \(X^0\) 样本与 \(X^1\) 样本的相似程度对 \(X^0\) 样本进行加权，以便在 \(X^0\) 上训练一个在 \(X^1\) 上无偏的模型。下面是领域适应学习器过程的概述

\[\begin{split}\hat{\mu}_0 & = M_1\left(Y^0 \sim X^0, \text{weights}=\frac{g(X^0)}{1-g(X^0)}\right) \\ \hat{\mu}_1 & = M_2\left(Y^1 \sim X^1, \text{weights}=\frac{1-g(X^1)}{g(X^1)}\right) \\ \hat{D}^1 & = Y^1 - \hat{\mu}_0(X^1) \\ \hat{D}^0 & = \hat{\mu}_1(X^0) - Y^0 \\ \hat{\tau} & = M_3(\hat{D}^0|\hat{D}^1 \sim X^0|X^1)\end{split}\]

其中 \(g(x)\) 是对 \(P[T=1| X]\) 的估计，\(M_1, M_2, M_3\) 是合适的机器学习算法，\(|\) 表示数据集连接。

EconML 包提供了以下领域适应学习器实现：DomainAdaptationLearner

双重鲁棒学习器

参见 双重鲁棒学习用户指南。

非参数双重机器学习

参见 双重机器学习用户指南。

类层次结构

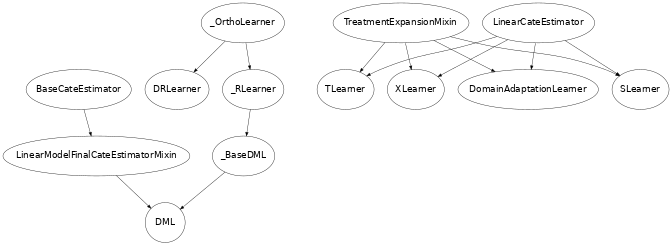
使用示例

请查看以下 notebooks

• 元学习器 Jupyter notebook.

• DML 示例 Jupyter Notebook,

• 森林学习器 Jupyter Notebook.