正交工具变量

它是什么？

正交工具变量是一套方法，用于在存在未观测混杂因素的情况下，借助有效的工具变量，使用任意机器学习方法估计异质处理效应。我们开发了一种估计异质效应的统计学习方法，将问题简化为最小化一个适当的损失函数，该函数取决于一组辅助模型（每个辅助模型对应一个独立的预测任务）。这种简化使得可以使用所有最新的机器学习模型（例如，随机森林、梯度提升、神经网络）。我们证明，估计的效应模型对辅助模型的估计误差具有鲁棒性，通过证明该损失函数满足 Neyman 正交性准则。我们的方法可以用于估计真实效应模型在更简单假设空间上的投影。当这些空间是参数化的，则参数估计是渐近正态的，从而可以构建置信区间。有关这些方法的更详细概述，请参见例如 [Syrgkanis2019]。

相关的估计器类有哪些？

本节描述了类 OrthoIV、DMLIV、NonParamDMLIV、LinearDRIV、SparseLinearDRIV、ForestDRIV、IntentToTreatDRIV、LinearIntentToTreatDRIV 中实现的方法。点击这些链接可以查看详细的模块文档和每个类的输入参数。

何时应该使用它？

假设您有观测数据（或来自 A/B 测试的实验数据），其中选择了某些处理/干预/行动 \(T\) 并观测到某些结果 \(Y\)。然而，数据集中并未记录所有可能影响 \(T\) 的选择，同时又可能直接影响结果 \(Y\) 的变量 \(W\)（即控制变量或混杂因素）。与此同时，如果您可以观测到一个变量 \(Z\)，该变量将直接影响处理，并且对结果的间接影响仅通过处理进行，则可以使用上述类在高维数据集上学习异质处理效应。换句话说，我们学习处理对结果的影响，作为一组可观测特征 \(X\) 的函数。

特别是，这些方法在具有意图处理结构的 A/B 测试中特别有用，实验者随机分配用户是否接收采取某项行动的推荐，而我们感兴趣的是下游行动的影响。

例如

from econml.iv.dr import LinearIntentToTreatDRIV
est = LinearIntentToTreatDRIV()
est.fit(y, T, Z=Z, X=X, W=X)
est.effect(X)

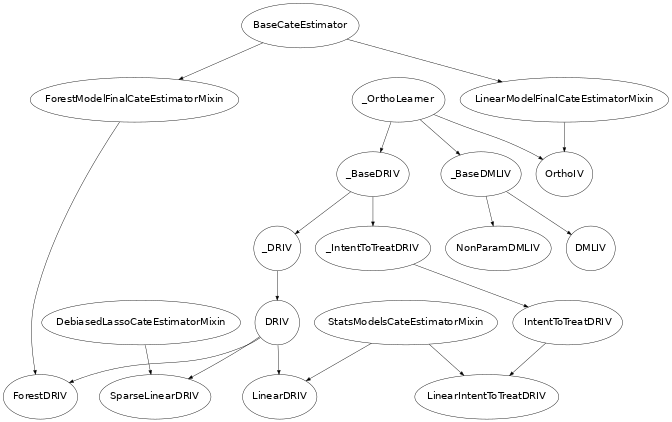
类层次结构

在本库中，我们实现了上一节中提到的几种方法的变体。实现的 CATE 估计器的层次结构如下。

使用示例

更多示例请查看以下 Jupyter Notebook：OrthoIV 和 DRIV 示例 Jupyter Notebook。